-
CP/CE1 : Les nombres entre 69 et 100

Si, lorsqu'on a dépassé les deux premières dizaines (de 1 à 10, puis de 11 à 20), les élèves enregistrent facilement le nom des nombres, il en va différemment pour les nombres compris entre 69 et 100.
Certains « bloquent » carrément et ne savent ni les lire, ni les écrire, et rares sont ceux qui, sachant les écrire, savent aussi les lire, alors que tous savent pourtant la plupart du temps les réciter à l'oral.Quelques idées en vrac pour les aider à mémoriser ces nombres aux noms bizarres issus des procédures de comptage de nos ancêtres.
Observation du Château des Nombres :
1. Construction
Sur une feuille format raisin (50 x 65), construire un grand tableau de 10 fois 10 cases, et le remplir case par case, avec l'aide des enfants, en commençant à 1 et en terminant à 100.Chaque enfant dicte un nombre :
Abel : Un... Béryl : Deux... Camelia : Trois... etc. jusqu'à Jacinthe qui dit : Dix, un Un et un Zéro (ou Une dizaine et zéro unité), puis Kader : Onze, un Un et un Un (ou Une dizaine et une unité), etc.
Ne pas accepter de nombres décomposés ainsi : "Soixante-sept, c'est six et sept» pour éviter la confusion entre les chiffres et leur valeur (six et sept, c'est treize et non soixante-sept).Au CP, on le complètera peu à peu, au fur et à mesure de l'apprentissage. Au CE1, on le complètera, selon les fichiers ou manuels employés, en une à quatre séances (les nombres de 0 à 10 ; les nombres de 10 à 20 ; les nombres de 20 à 69 ; les nombres de 70 à 100).
2. Pour mémoriser les nombres de 70 à 100 :
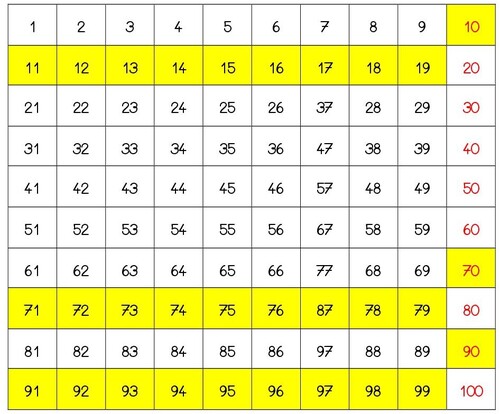
On y lit les nombres, dans l'ordre, et on remarque que les nombres dont le chiffre des dizaines est 1, 7 et 9 emploient les mêmes mots.
Pour aider à la mémorisation de ces mots, on colorie les cases de la même couleur (par exemple cases jaunes pour les nombres de 10 à 19, 70 à 79, 90 à 99).
3. Jeu du château des géants
On peut parfaire la mémorisation en jouant régulièrement au jeu des volets fermés : 100 géants sont venus dormir dans le château, certains dorment encore.
- Avec des "post it", on cache en secret certains nombres du tableau, pendant que les enfants mettent leur tête dans leurs mains.
- Les enfants qui savent dire et écrire le nombre qui est caché derrière gagnent le "post it".
- Bien sûr, on choisit un maximum de volets fermés dans les lignes de 60 à 99.
Lier Numération, Calcul, Mesures et Monnaie :
On peut aussi assurer la connaissance lexicale par la connaissance mathématique : 80 s'appelle quatre - vingts parce qu'on l'obtient en comptant 4 fois 20 ; 70, c'est 60+10, 71, 60+11, etc.
En assurant le calcul par des :
- jeux de monnaie :
→ marchande: payer 63 €, payer 73 € ; payer 82 €, payer 92 € ; ...
→ distributions : « Je vais donner 4 pièces de 2 € à chacun, combien aurez-vous ?... et avec 4 billets de 20 € ?... et avec 4 pièces de 2 € et une pièce de 1 € ?... et avec 4 billets de 20 € et un billet de 10 € ?... etc.)
→ partages : « J'ai 6 € en pièces de 2 €, à combien d'enfants puis-je en donner une ?... J'ai 60 € en billets de 10 €, combien d'euros puis-je donner à chacun des enfants d'un groupe de trois enfants ?... Si j'ai 70 € en billets de 10 €, combien puis-je en donner au même groupe, combien restera-t-il de billets ?
- mesures en cm
→ dans la cour ou sur de grands objets
→ lecture de la règle du tableau et repérage de nombres
→ nombres de réglettes Cuisenaire de 10 cm dans 60 cm ?... dans 70 cm ?... etc.
- calculs avec des bûchettes par paquets de 10 et bûchettes à l'unité :
→ 60 + 5 et 60 + 15 ; 80 + 6 et 80 + 16 ; etc.
→ 98 - 8 ; 98 - 10 ; 98 - 18 ... 77 - 7 ; 77 - 10 ; 77 - 17 ; etc.
La commande de doigts
- Je demande par exemple :
→ une commande de 60 doigts (donc 6 enfants qui constituent le groupe A),
→ une de 80 doigts (donc 8 enfants qui constituent le groupe B),
→ une de 13 doigts (1 enfant qui montre 10 doigts et 1 qui ne lève que 3 doigts qui constituent le groupe C)
→ et une de 16 doigts (1 enfant qui montre 10 doigts et 1 qui ne lève que 6 doigts qui constituent le groupe D).
- On réunit les groupes A et D (60 et 16) d'une part et les groupes B et C (80 et 13) d'autre part.
- Les élèves doivent écrire en chiffres et en "mots" le nombre de doigts levés de leur groupe.
Fréquence des activités :
Ces activités sont à mener de manière très régulière jusqu'à ce que tous les élèves arrivent, après réflexion, à lire et écrire un nombre compris entre 60 et 99.
La commande de doigts
Elle peut être utilisée en échauffement au début de la séance quotidienne d'EPS (ne me dites pas que vous ne faites pas EPS tous les jours ou je vous fais les gros yeux !).
Le jeu du château
Il demande d'abord d'utiliser de une séance à quatre séances de mathématiques étalées dans le temps ou consécutives à sa construction.
Quand il est construit, même partiellement, sa lecture dans l'ordre doit être quotidienne, en établissant un tour de rôle pour la lecture (l'élève 1 lit le premier nombre, l'élève 2 le deuxième, etc.). On peut choisir de faire uniquement lire les nombres, ou de demander que chacun lise ainsi : « Un, c'est une unité... Deux, c'est deux unités... etc. Dix, c'est une dizaine et zéro unité... Onze, c'est une dizaine et une unité... »
Quand les élèves commencent à ne plus trop hésiter sur la lecture des nombres de 60 à 99, le jeu des volets fermés pourra servir de rituel au début de la séance quotidienne de mathématiques.
On pourra ressortir et corriger ce château des nombres lorsqu'on étudiera les nombres de 101 à 200. Les élèves comprendront ainsi intuitivement les règles de la numération décimale au lieu d'être dans un « par cœur » qui les bloque dans leur compréhension mathématique de ce système.
Lier Numération, Calcul, Mesures et Monnaie
C'est un état d'esprit à acquérir. Cela se fait au quotidien, lors de chaque séance de mathématiques. On tisse des liens entre les sous-domaines pour que la « toile » se renforce et devienne de plus en plus dense, et que les connaissances d'un sous-domaine servent à construire les connaissances des autres.
Je n'ai pas inclus le domaine Résolution de problèmes car, dans mon esprit, il est mis en œuvre lors de chaque séance quotidienne de mathématiques.
 Tags : numeration, nombre, lire, écrire
Tags : numeration, nombre, lire, écrire
-
Commentaires
2EmilieMercredi 16 Juin 2021 à 22:58
Beaucoup d'idées très intéressantes! Je dévore chaque article de votre blog. Mille fois merci pour tous ces partages.
-
Jeudi 17 Juin 2021 à 09:48
-
 Suivre le flux RSS des commentaires
Suivre le flux RSS des commentaires
 Ajouter un commentaire
Ajouter un commentaire
L'École Primaire comme je voulais la raconter







Merci pour ces idées très intéressantes. Je vais faire les nombres entre 69 et 100 en période 2 et ça va m'être bien utile. Merci beaucoup!