Merci à Bayard Presse pour cette image qui me rend bien service...

Apprendre à poser des divisions, à partir de situations de partage simples, inscrites au programme dès la maternelle, c'est tout à fait possible, aussi bien au CE1 qu'au CE2.

Voici les étapes à respecter, dans un CE2 qui n'aurait pas eu accès à cette opération les années précédentes, dès qu'on a introduit les doubles en calcul mental :

Les partages en 2 parts égales :

1) la moitié d'un nombre pair (les partages de petites quantités, sans reste) :

D'abord jusqu'à 20, puis jusqu'à 40... puis celles des dizaines jusqu'à 100 (pour pouvoir introduire assez vite la division par 5 ensuite).

⇒ on utilisera tout d'abord uniquement le terme "partagé en 2".

⇒ puis on emploiera en l'expliquant "divisé par 2", en le doublant toujours de l'expression "partagé en 2"

⇒ enfin, quand les élèves auront bien fait le lien entre la manière d'obtenir le résultat mentalement, sans manipulation, et la table de 2 qu'ils connaissent maintenant par cœur, on ajoutera l'expression « En ..., combien de fois 2 ? » qui nous sera très utile à l'étape suivante.

Exemple : Rechercher la moitié de 24

« 24 divisé par 2, c'est 24 partagé en 2, c'est 2 fois 10 et 2 fois 2,

alors c'est 12. 24 divisé par 2, c'est 12. »

Pendant cette première étape, on ne fera que des calculs en ligne : 24 : 2 = 12

2) les même partages avec reste :

Jusqu'à 21, d'abord en calcul mental (pour bien fixer l'intérêt de connaître la table de 2 par cœur) puis, devant la difficulté de d'organisation sur l'ardoise, très vite, par écrit.

17 : (partagé en 2, on dit "divisé par 2"), c'est 8 fois 2 et il reste 1

qu'on écrira :

17 : 2 = 8 et il reste 1

C'est là qu'apparaît l'intérêt de la division posée, qu'on expliquera comme ceci (les mots dividende, diviseur, quotient et reste, sont à introduire petit à petit, sans exiger leur restitution, pour ne pas affoler) :

♥ un exemple tiré du guide pédagogique de  CP : Cahiers de Mathématiques (5) :

Je vous présente la machine à partager (avec un exemple pour adulte, ne vous affolez pas) !

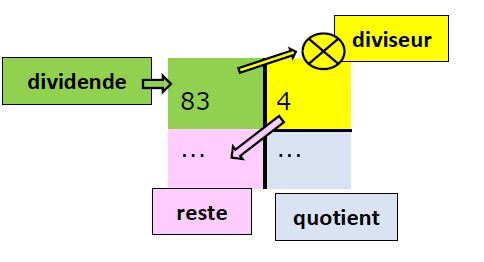
Ici, on pourra dire :

« Je mets 83 billes dans la case verte, celle où je range les objets à partager, on dit aussi le dividende, et, dans la case jaune, la case du diviseur, j'indique à la machine à partager, on dit aussi diviser, que je veux partager, diviser, cette quantité en 4 parts égales.

Puis je me demande : « En 83 combien de fois 4 ? »

Je trouve 20 fois 4 pour avoir 80, alors j'écris 20 dans la case bleue, la case du résultat, du quotient, juste sous le 4 et le signe x pour qu'on comprenne bien que c'est 4 fois 20 qui est égal à 80.

Mais il me reste 3 billes que je n'ai pas pu partager alors j'écris 3 dans la case rose, la case du reste,  juste sous la case verte, car c'est le côté des objets qui n'ont pas encore été partagés.

♥ Un exemple pour avancer à petits pas

Ça peut paraître très compliqué a priori mais si on commence avec la table de 2 seulement et des quantités inférieures à 20, en donnant l'impression aux élèves que ce sont eux qui inventent la technique, ça se fait presque tout seul.

Regardez, par exemple, avec 17 : 2, sans matériel (nous nous en servirons seulement après, pour vérifier si notre technique fonctionne).

◊ « Nous avons 17 pièces d'or que nous voudrions répartir de manière égale dans 2 coffres... Pour ne pas nous perdre, si nous écrivions les nombres dans un tableau ? Où mettrions-nous le nombre 17 et le nombre 2 ?

Petit débat de quelques secondes, aboutissant à la « décision » suivante :

Si nous mettions 17 dans la dans la case de gauche et 2 dans la case de droite, ce serait dans le sens de la lecture : « En 17, combien de fois 2 ? »

 Et si nous ajoutions le signe x pour être sûrs de ne pas oublier que nous cherchons à savoir « combien de fois 2 » ?... à côté du 2...

Nous pourrions aussi mettre des couleurs ? Je vous propose du vert pour la case des objets pas encore partagés et du jaune pour la case de la règle de partage (parce que dans le vert, il y a du jaune)...

(Faire au fur et à mesure pour obtenir peu à peu ceci :)

– Voilà. Qui peut me relire ce codage ?...  « Dans la boîte verte, nous avons 17 pièces d'or à partager  et la règle de partage, c'est « Combien de fois 2 ? ».

– Oui, nous dirons que 2, c'est le diviseur. 

– Très bien... Qui connaît la réponse à la question « En 17, combien de fois 2 ? » ?

– 8, parce que 2 fois 8, 16 ! Et 16, c'est presque 17.

– Oui, c'est 8 pour chacun parce que 2 fois 8 = 16. Mais il reste une pièce d'or qu'on ne peut pas distribuer.

–  Où pourrions-nous écrire ce résultat, ce quotient, comme disent les mathématiciens ?...

Petit débat de quelques secondes, aboutissant à la « décision » suivante :

– Et si nous écrivions la part de chacun sous le 2 pour bien voir que c'est 2 fois 8 qui font 16 et le reste sous le 17 puisque c'est le côté des pièces qui ne sont pas encore partagées ? Et puis nous mettrions des couleurs... Quelle couleur qui aurait un rapport avec le vert et le jaune pour le quotient, c'est-à-dire la part de chacun ? 

Petit débat de quelques secondes, aboutissant à la « décision » suivante :

– Bleu pour le quotient, c'est-à-dire la part de chacun, parce que du bleu mélangé avec du jaune, ça fait du vert. Et pour le reste ? Il faudrait une couleur qui dise que c'est impossible à partager pour le moment... Une couleur qui serait celle de l'empêchement, de l'interdit...

Petit débat de quelques secondes, aboutissant à la « décision » suivante :

Et rose pour le reste parce que c'est un peu comme du rouge, la couleur de l'empêchement, de l'interdit (pour le moment, nous n'arrivons pas à partager une pièce d'or en deux, c'est interdit).

(Faire au fur et à mesure pour obtenir peu à peu ceci :)

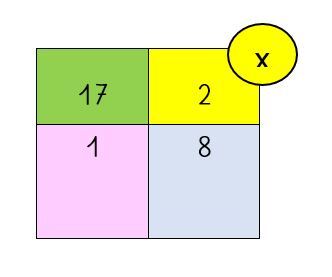
– Il ne nous reste plus qu'à effacer les traits qui ne servent à rien... Quels traits servent à quelque chose ?

Petit débat de quelques secondes, aboutissant à la « décision » suivante :

– D'accord. Nous allons en garder 2 : un pour séparer le côté des objets pas encore partagés du côté de la règle de partage, du diviseur et un autre pour séparer la règle de partage, le diviseur, du quotient, du résultat obtenu.

(Faire au fur et à mesure pour obtenir peu à peu ceci :)

– Nous n'avons plus qu'à tout relire ensemble : « Nous avons 17 pièces d'or à partager. La règle de partage est « Combien de fois 2 ? ». Nous disons : « En 17, combien de fois 2 ? ». Nous savons que 2 fois 8 = 16, alors nous écrivons 8 dans la case bleue, la case du quotient, du résultat. Mais il reste 1. Nous écrivons 1 dans la case rose, du côté des objets que nous n'avons pas pu partager.

En réutilisant tout de suite la machine, qu'on aura présentée vide au tableau,

pour 12 pièces (pour qu'apparaisse le reste égal à zéro tout de suite), puis 15, puis 8, ..., les élèves prennent peu à peu confiance en eux, surtout si on les encourage et on les félicite au moindre progrès, et ils oublient que « la division, c'est très difficile » et leur maîtresse aussi...

3) Les partages de grandes quantités :

Ici, nous nous retrouvons dans le domaine privilégié du calcul écrit, celui où la technique dite « de la potence » a tout son intérêt. Cette technique, à peine effleurée au CP, déjà un peu utilisée au CE1, doit arriver à un niveau de maîtrise en fin de CE2.

Voyons par exemple, le calcul proposé dans le cahier CE2 : Fichier de Mathématiques (1).

Lorsque cette séance sera menée en classe, seul le problème sera écrit au tableau. Si les élèves ne le proposent pas eux-mêmes, nous leur proposerons de nous servir de la « machine à partager ».

Le souci viendra de la quantité à partager, bien supérieure à 20... Notre rôle sera alors de les aider à suggérer que nous pourrions peut-être d'abord ne nous occuper que des dizaines. Ce qui donnerait à peu près cela :

« Puisque nous ne connaissons pas la table de 2 jusqu'à 118, peut-être pourrions-nous nous occuper que des centaines pour le moment ? Combien avons-nous de centaines ?

– Une seule...

– Savons-nous partager 1 en 2 parts égales ?

– Non, pas pour le moment. Mais nous savons que 1 centaine, c'est 10 dizaines. Et ça nous saurons le partager en 2.

– Attention, dans 118, n'y a-t-il que 10 dizaines ?

– Non, il y a 1 centaine et 1 dizaine, cela fait 11 dizaines.

– Je vais repasser les deux chiffres 1 en rouge, comme ceci. Et maintenant, c'est simple : « En 11, combien de fois 2 ? »  Oui, c'est 5. 2 fois 5 dizaines = 10 dizaines et il reste 1 dizaine. Nous écrivons tout cela en rouge pour ne pas nous perdre.

(Faire au fur et à mesure pour obtenir peu à peu ceci :)

– Et maintenant, occupons-nous des unités ? Combien en avons-nous ?

– 8.

– Nous sommes d'accord, mais nous avons aussi la dizaine qui nous restait... Alors, combien d'unités en tout ?...

– 1 dizaine et 8 unités, c'est 18 unités en tout.

– Écrivons le chiffre 8, en noir, à droite du chiffre rouge de la dizaine qui reste. Comme ceci. Et maintenant, quelle question devons-nous nous poser ?

– « En 18, combien de fois 2 ? »,

–  C'est ça. Le quotient, vous le connaissez bien sûr ?

– C'est 9, 9 fois 2 = 18.

– Où dois-je écrire ce 9 et de quelle couleur ? J'écris 9 en noir à la droite du 5 rouge des dizaines. Nous lisons 59.

–  En 118, combien de fois 2 ? 59 fois 2 = 118. Malo et Marie auront 59 bielles chacun.

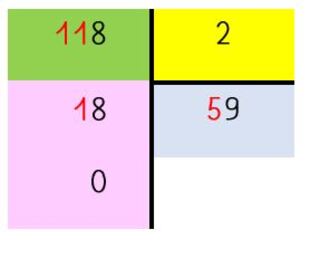
– Et y a-t-il un reste ?... Non, il n'y a pas de reste. Écrivons 0 dans la case du reste, en-dessous du reste partiel, 18. Comme ceci :

(Faire au fur et à mesure pour obtenir peu à peu ceci :)

En reprenant ensuite plusieurs fois ce schéma ensemble, puis de manière guidée, nous commencerons à atteindre un semblant de maîtrise qu'il n'y aura plus qu'à entretenir et perfectionner ensuite.

Les partages en 5 parts égales :

 La semaine suivante, c'est le tour de la table de 5 d'être à l'honneur. Nous reprenons le même schéma :

1) les partages de petites quantités, sans reste

En calcul mental, jusqu'à 50, simplement, car c'est juste pour fixer les résultats de la table de 5.

2) les même partages avec reste :

Jusqu'à 54, d'abord en calcul mental (pour bien fixer l'intérêt de connaître la table de 5 par cœur et les restes possibles : 0, 1, 2, 3 et 4) puis, devant la difficulté de d'organisation sur l'ardoise, très vite, par écrit.

Nous ressortirons alors notre « machine à partager » que nous commencerons à nommer plutôt « division posée »... ou « technique de la potence », mais dans ce cas-là, il faudra expliquer ce qu'est une potence...

Pour les nombres inférieurs ou égaux à 54, la maîtrise en autonomie de cette technique devrait être presque acquise pour tous. Peut-être pas jusqu'à supprimer les couleurs mais presque.

3) Les partages de grandes quantités

En revanche, c'est sûr, à part deux ou trois cas de vrais matheux par ci par là, pour les partages de quantités supérieures à 50, notre présence sera encore très utile.

Le fait de s'organiser pour partager d'abord les dizaines, puisque pour le moment le champ numérique n'atteint pas 500, puis les unités renforcera la compréhension de la règle décimale : 1 centaine = 10 dizaines, 1 dizaine = 10 unités.

Quant au fait de ne pas écrire les soustractions à l'intérieur de la division, outre le fait que ça allège la présentation, il permet de bien poser la règle qu'un reste est toujours inférieur au diviseur et de renforcer le calcul mental (ici les compléments de 5 jusqu'à 9).

Les autres partages en parts égales :

Ces trois étapes seront reprises chaque semaine, jusqu'à la Semaine 14, chaque fois avec une table différente.

Après ces dix semaines, la quasi-totalité des enfants n'aura plus d'appréhension à l'idée de se servir de la « machine à partager » que tous nommeront « division posée » et utiliseront sans les couleurs... Il sera temps de passer à la division par 10 (Semaine 15), puis à la division par 100 (Semaine 16), puis à celle par 20, 30, 40, ..., 90 (Semaine 19) et enfin, de la Semaine 21 à la fin de l'année, en sachant que la maîtrise ne pourra être exigée, à la division euclidienne, bien sûr, par un nombre à 2 chiffres...

Tout ceci aidera grandement les élèves à aborder le Cycle 3, en espérant que nombreux seront les collègues qui n'attendront pas le mois de mai du CM1 et même parfois du CM2 pour réaborder une technique que des élèves de 8 à 9 ans peuvent maîtriser si :

→ nous les accompagnons et nous les soutenons

→ nous avançons à petits pas, tout au long de l'année scolaire

→ nous savons nous contenter d'une maîtrise partielle pendant une grande partie de l'année

soit, en quatre mots :

→ nous leur faisons confiance !